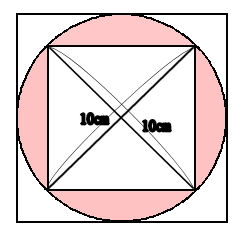
芸術的な難問 良問数学 中2数学 複雑な多角形 角の和応用問題 今回は複雑な多角形の角の和の問題とその考え方です 星型など複雑な図形の角の和を求めるとき三角形の外角の定理やブーメラン型四角形の角リボン型ちょうちょ型の三角形の角の考え方が役立ちます円と正方形 右の図で,円の面積は正方形の面積の157倍です。 例題 (1) 右の図1 の斜線部分の面積を求めなさい。ただし,円 周率は314とします。 (立命館中) (2) 右の図2 は円の中に,1 辺4cm の正方形がぴったりと 入ったものです。斜線部分の面積を求め 正方形abcdの内部にp,pb=1,pd=7,pc=5 このとき,正方形の面積を求めよ。 この問題を一瞬で解けると言われたのですが、どのように解けるのでしょうか? 私にはまったくわかりません。 どなた様かご教授ください。
算数の 図形から面積を求める問題に悩んでます 四角形abcdと四角 Yahoo 知恵袋
円 正方形 面積
円 正方形 面積-そうすれば、ア・イそれぞれ面積を変えずに 境界線をひき直すことができます。 まとめ お疲れ様でした! 等積変形についての問題は 等しい三角形を見つける 面積が等しくなるように作図する この2点をしっかりをおさえておけば大丈夫です!正八角形の対角線で囲まれた面積 東海中 08 円内を転がる正方形 雙葉中 07・6 転がる正方形 清真学園中 06・後期・3 長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中 16・第1日・9 転がる正方形 駒場東邦中 16・3



半円 算数解法の極意
円とおうぎ形⑹ 弓形の面積 16 16 次の図は、1辺8㎝の正方形ABCDと、直径8㎝の円を4個組み合 わせた図形です。色のついた部分の面積を求めなさい。ただし円周率 は314とします。三角形fbjの面積を①とすると、台形afjiの 面積は③。 三角形fbjと三角形aie、三角形dlh、 三角形ckgは合同、台形afjiと台形eild、 台形hlkc、台形gkjbは合同、三角形abe と三角形ebg、三角形ged、三角形dgcは 合同なので、正方形abcdの面積は⑳、 正方形ijklの面積は④ すると、上の正方形は、 となり、一辺が4cmということになり、面積は16cm 2 です。
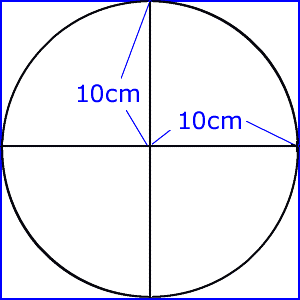
小さな正方形になる、ピッタリ重なるから、半分の面積だ。 答え 32c㎡ 考え方2 中の正方形の4分の1の面積をもとめ、その4倍をすれば良い。 4分の1の三角形の、たてと横のながさは、4cm だから が小さな三角形で その4倍が正方形だから 扇形と正方形IPSJ Magazine Vol45 No1 Jan 04 49 プログラムの入力は,次のような形式になる. n x1 y1 x2 y2 xn yn 最初の行が頂点の個数nである.nは100以下と定 められている.2行目以降に多角形の頂点の座標を順 に並べてある.それぞれのkに対して,k番目の頂点採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く
円積問題 えんせきもんだい quadrature of a circle 円の正方形化,すなわち与えられた円と等しい面積の正方形を作図することをいう。 古代においてこの問題は,重要な未解決の作図題と考えられていた。 しかし,与えられた円の周と同じ長さの直線,あるいは与えられた円と同じ面積の正方形をΦ600の内接する正八角形の1辺の長さを求めたかった ご意見・ご感想 円の半径r=300でのn=8の多角形の1辺の長さaはではなくて?ではないでしょうか。 keisanより r=300の時、辺の長さがとなるのは、 円に外接する正多角形と考えられます。円の面積学習における学習の流れ (子ども の音符の流れ)を次のように考えた。 ① 円の面積は円周内部の面に存在し,円 の半径と依存関係にあることに気づく。 ② 円の面積は,その円の半径を一辺とす る正方形の面積の2倍より大きく4倍よ



円の中の正方形



頭の体操 図形編
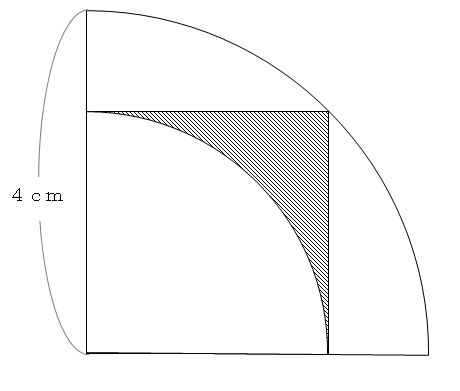
この部分の面積は以下のように求めます。 この赤いおうぎ形は大きな円の4分の1になっています。 円の半径は正方形の一辺と同じなので1cmです。 従ってこのおうぎ形の面積は1×1×314÷4=0785ですね。 そこからこの青い三角形を引きます。 この青い三角形図形 面積 求め方 から,考え方をお伝えしております。受講生の支持トップ級・カリスマ講師年11月1日より、数学の授業動画を取り上げて 第131問 正方形の面積 図形ドリル 45度 6年生 正方形 直角二等辺三角形 ★★☆☆☆☆(小学4〜5年生対象) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げて




Twitterで拾った問題 半円に接する2つの正方形 オンライン講師ブログ



Math 算数のコツ 18 円の中の正方形 働きアリ The 2nd
大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え ㎠ 面積④ 重なりや移動でできた面積 例題5 長方形と正方形が下の図のように重なっています。色の付いた部分の面積を求めなさい。 解説円周や弧の長さ、円の面積やおうぎ形の面積は 「円周率の倍数 」です。 円周率が314のこの問題では、 弧の長さ157cmを「5×314」の形に変えておくことができます。 はじめにありました「覚えておきたい」で、 「2×円周率~9×円周率」の値 が頭に入ってこの正三角形の一辺は円の中心点より六角形の各点へと 引かれた線であるため長さはRとなる。 これより三角形の面積は 2 円に内接する六角形の面積はこれを6倍したものである。 円に外接する正六角形も同じ大きさの正三角形を6こ組み合わせたものである。




正方形に内接する円と四分円に囲まれる面積 高校時代に友人から聞いて 数学 教えて Goo
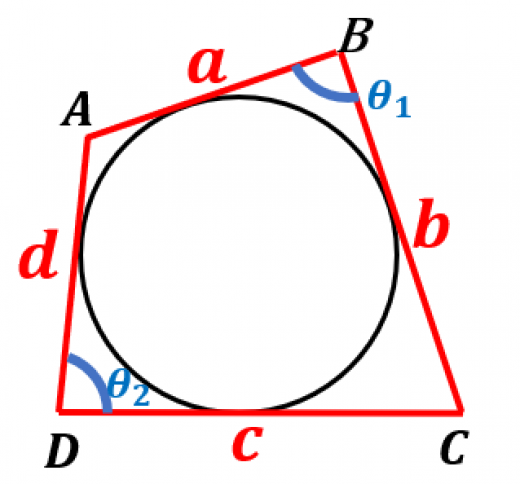



円に外接する四角形の重要な2つの性質 高校数学の美しい物語
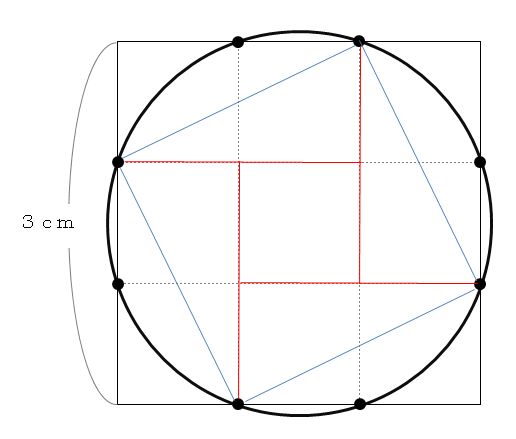
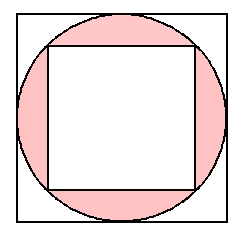
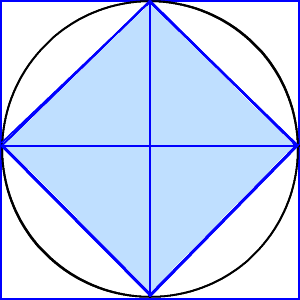
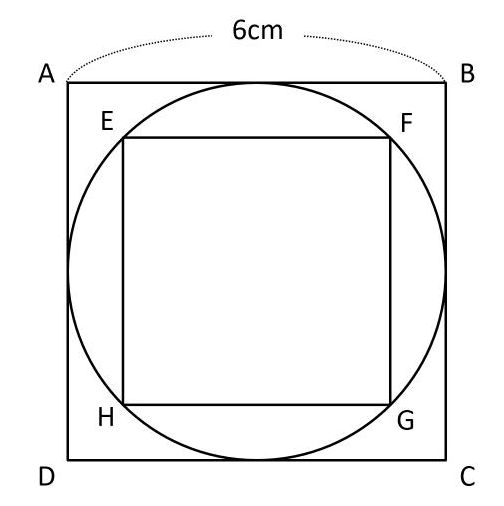
ABを直径とする円を書くと、黒くぬった部分の面積は何c㎡になりますか。円周率は314とします。 → 解答 問題7 1辺が10cmの正方形ABCDの各辺の真ん中の点を結んでできた正方形EFGHがあります。 円の面積=赤い正方形×314 なのです。 問題を解いてみましょう。 まず、図をかき直します。 円全体をかき、外接する正方形をかく。 公式の意味がわかるように外接した正方形を4等分。 すると、どうでしょう。 この答えをよく見てみると、 $18\pi36$ のうち、 $36$ は正方形の面積を表していると考えられます。では $18\pi$ は何かというと、円の面積は $36\pi \mathrm{ cm }^2$ なのだから、これは半円の面積だと考えることができます。



円の面積 1 5
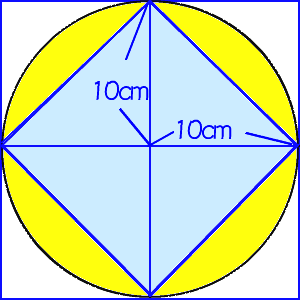



6年算数 円の面積 1 アニメでわかる教え方
円とおうぎ形⑺ 正三角形が関係する問題 1 ステップ1 面積を求める① 1 図のように、正方形ABCDの中におうぎ形を2個かき円の面積を求めるためには、まず円の半径を求めなければ ならない。正方形の一辺は円の中心をとおっていないので 直径ではない。この円の面積はこの円の中心をとおる、正 方形の対角線である。すなわち、半径はこの対角線の半分 の長さである。解法の見通し 求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! χ=(正方形)-(a+b+c+d)
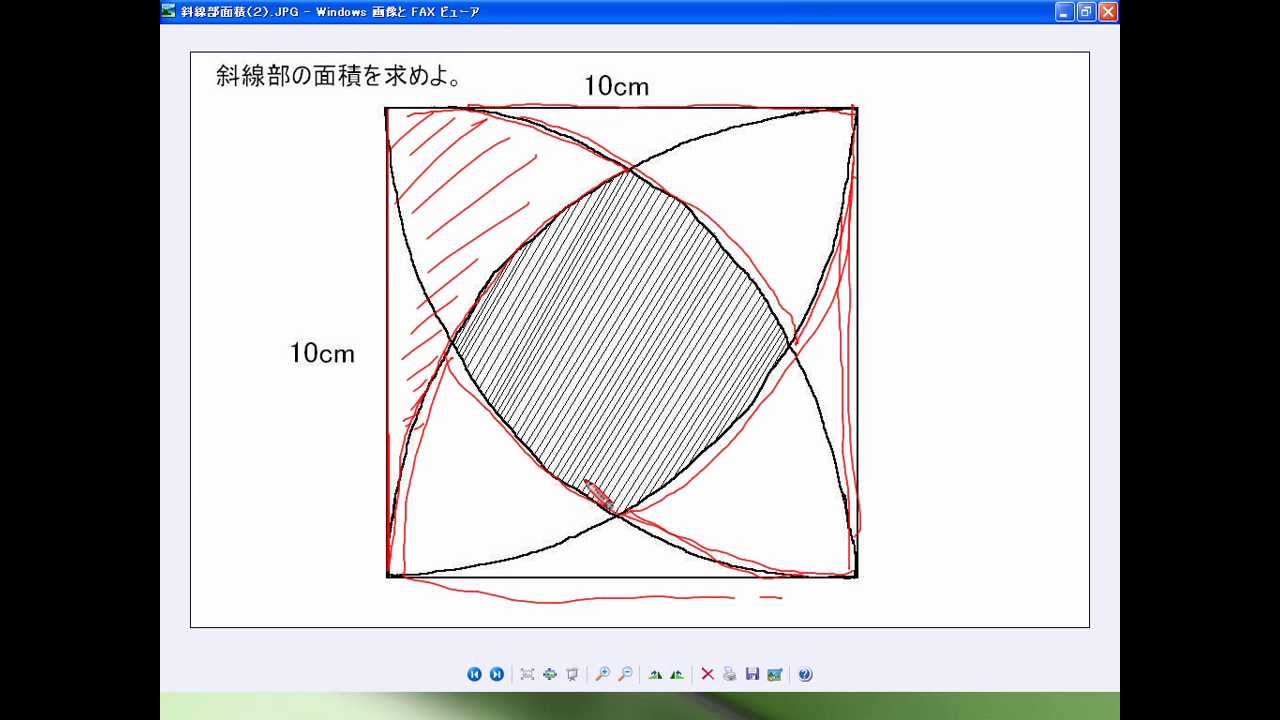



斜線部の面積 4 1辺10cmの正方形の場合 Youtube




円の面積 練習応用 Youtube
正方形の中に図のように四分円が3個と、等円が2個あります。等円は正方形と四分円に接しています。 ・等円の直径が1cmのとき、正方形1辺の長さを求めてください。 ・斜線部分の面積を求めてください。 ただし、円周率はπとします。第27問 正方形5個の面積 図形ドリル 5年生 6年生 正方形 直角三角形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題



この数学の問題がわかりません 問題 画像の図は正方形と半円を組み合わ Yahoo 知恵袋



半円 算数解法の極意



円の面積の求め方についてです 正方形のなかに直径9cmの円があ Yahoo 知恵袋
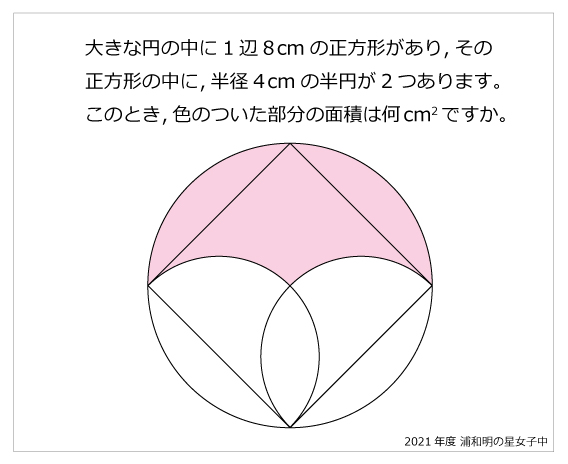



今年の1問 21年浦和明の星女子中 円と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦




長女の中学受験 算数の復習で最低限覚えておきたい図形 円と正方形の話を復習しました Pi Sukeのネットな生活



求積問題 正方形と扇形
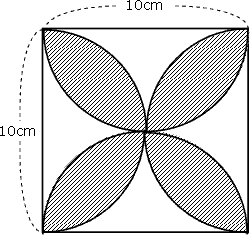



面積の求め方 算数の教え上手 学びの場 Com



Pronity 57 球の直径 円周 面積 体積に合わせた 正四面体 正三角形と立方体 正方形の比例



正方形から円を引いた面積 灘中学 2007年 これが中学入試に出た図形問題




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
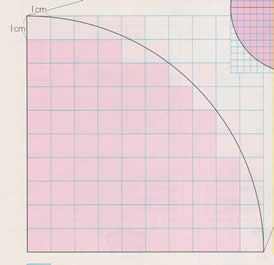



円の面積 2 5




4つの円のすき間の解答と解説 多目的ルーム 楽天ブログ



入試に使える算数の基礎 半径 半径



入試に使える算数の基礎 半径 半径



図は円の中に正方形が内接しているものですが このような円の面積 Yahoo 知恵袋




Mondai55




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
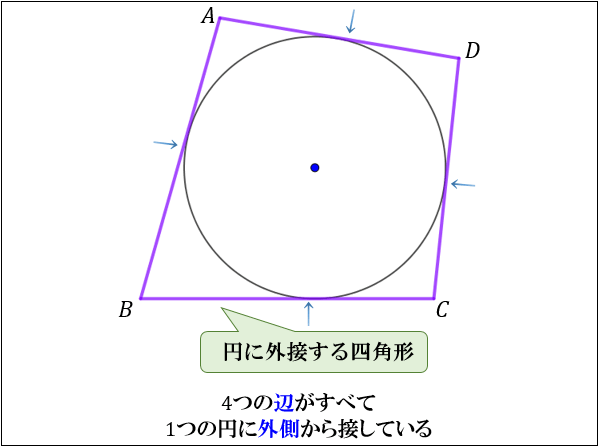



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ



正方形内の円 開智中学 2010年 どう解く 中学受験算数




円の面積 円周の長さ わさっきhb



円の中の正方形



算数の 図形から面積を求める問題に悩んでます 四角形abcdと四角 Yahoo 知恵袋




円の面積 算数用語集



正方形とおうぎ形 奈良学園中学 算数入試問題 1998年 どう解く 中学受験算数
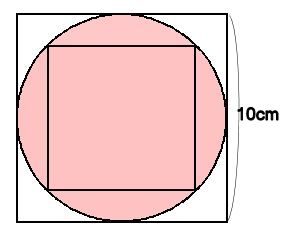



円の中の正方形




面積の求め方 算数の教え上手 学びの場 Com
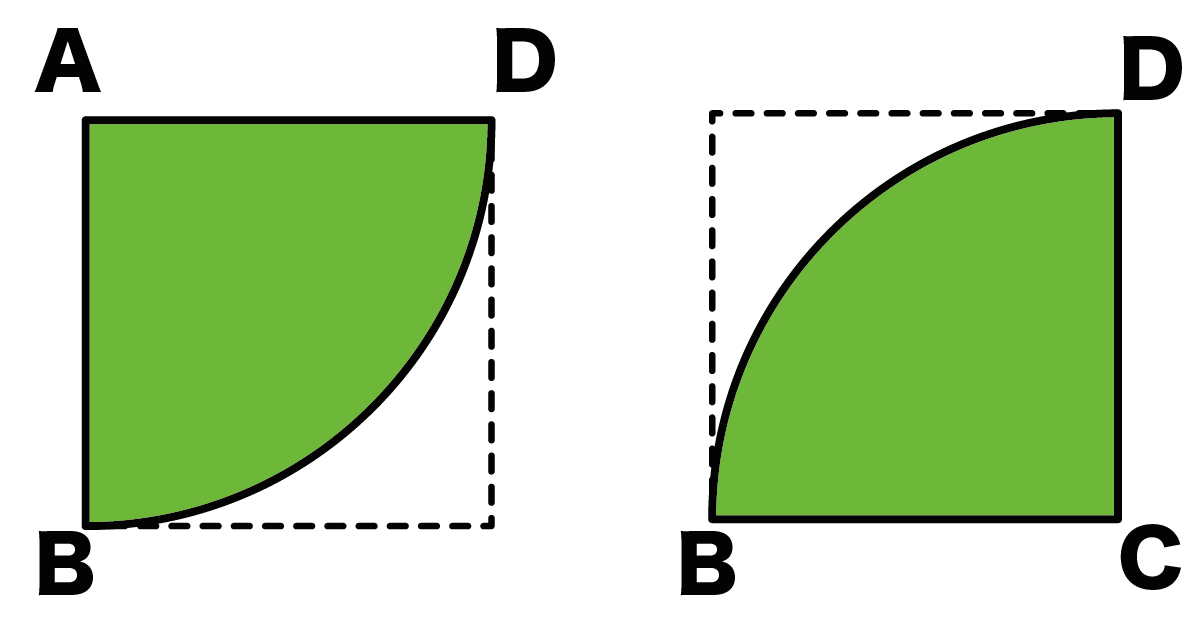



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



雑学のソムリエ 円の面積を直径で表す
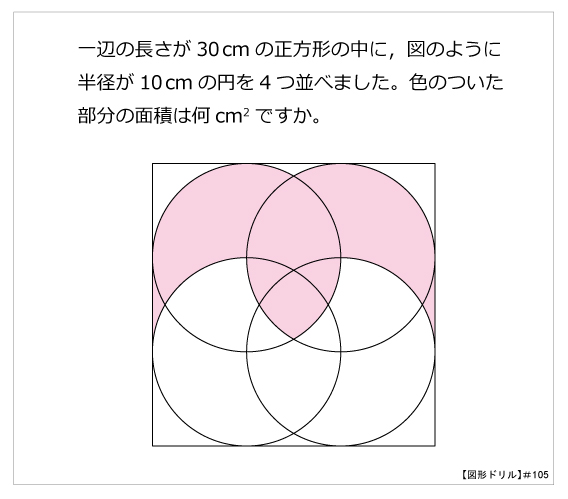



図形ドリル 第105問 正方形と円 算数星人のweb問題集 中学受験算数の問題に挑戦




Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 養成講座




15年度 愛光中学校 算数 1 6 面積



正方形と円 2015年 開成中学の面積問題から 図で解く算数
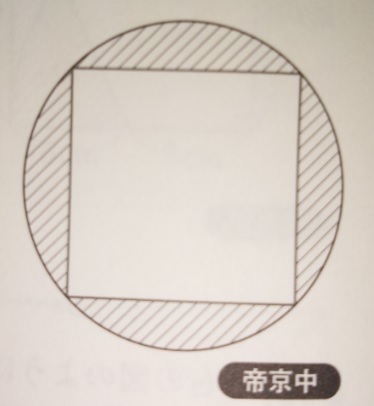



円と正方形で覚えるルールはこの2つ 中学受験 塾なし の勉強法
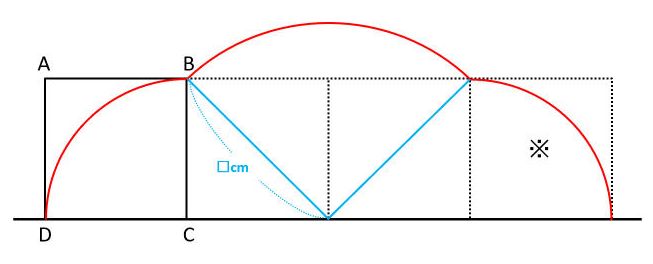



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
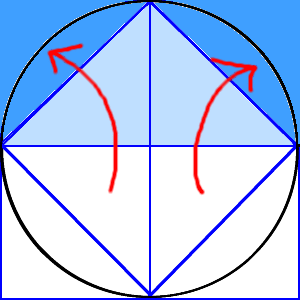



6年算数 円の面積 1 アニメでわかる教え方
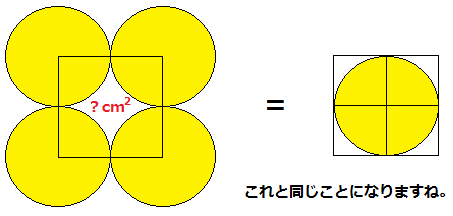



4つの円のすき間の解答と解説 多目的ルーム 楽天ブログ




収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良



図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト
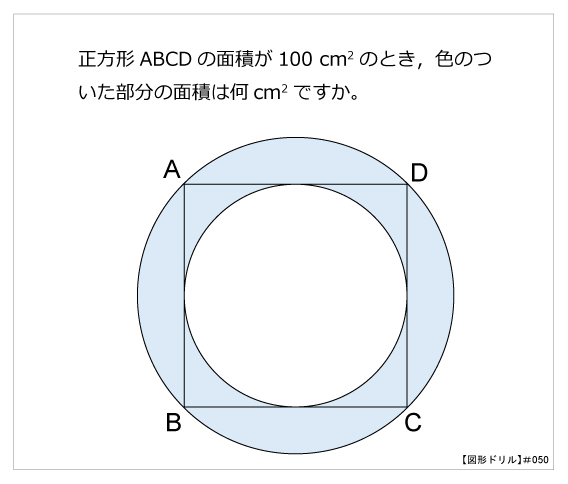



図形ドリル 第50問 内接円と外接円 算数星人のweb問題集 中学受験算数の問題に挑戦



6年算数 円の面積 1 アニメでわかる教え方



No 086 巻頭言 半径は計算せずに円の面積を求める Fumiononaka Com Newsletter




円積問題 Wikipedia



6年算数 円の面積 1 アニメでわかる教え方
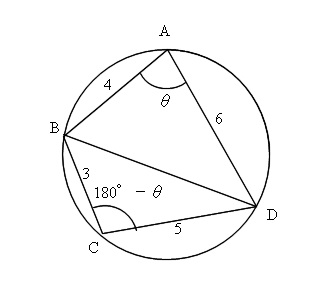



円に内接する四角形の面積の求め方と定理の使い方



円の面積 面白ゼミナール




半円に内接する2つの正方形の面積の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog



1
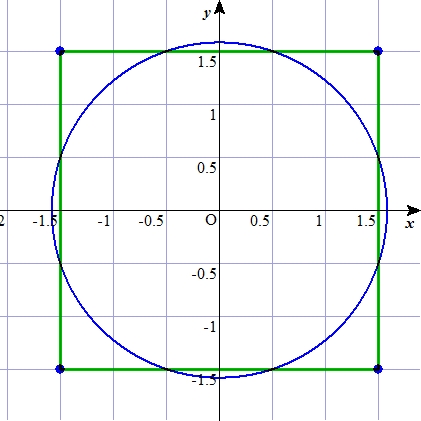



正方形と円の面積 コ コ ロで遊ぶ算数教室
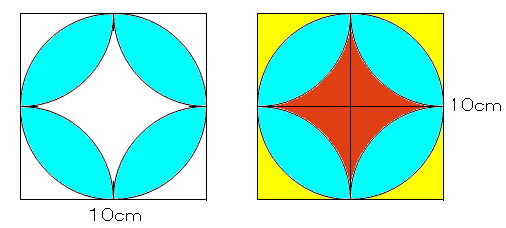



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素
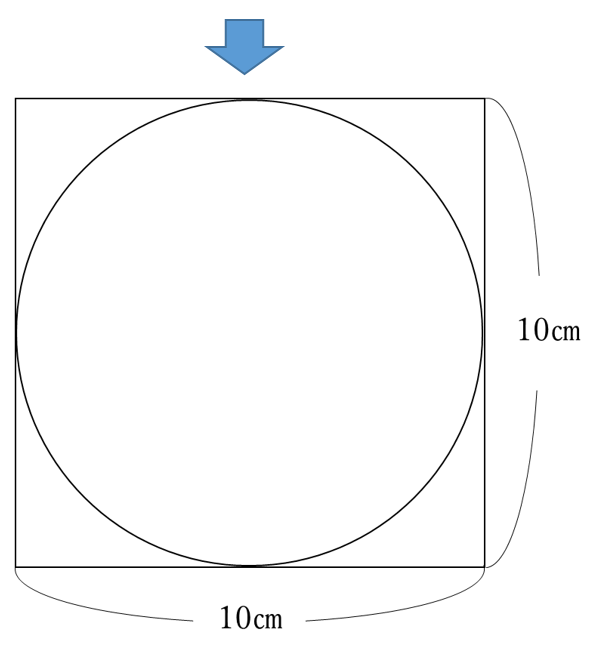



円の相似を利用した面積の計算 中学受験プロ講師ブログ



小学生向け難問その 2 解答 途中まで While Im Automaton




はっぱ型 の図形の面積 身勝手な主張
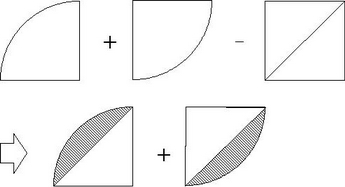



0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾




円の面積 その2 家庭学習レシピ




超頻出 正方形の中にある正方形の面積 問題 恋する中学受験 大学受験を見据えた中学受験
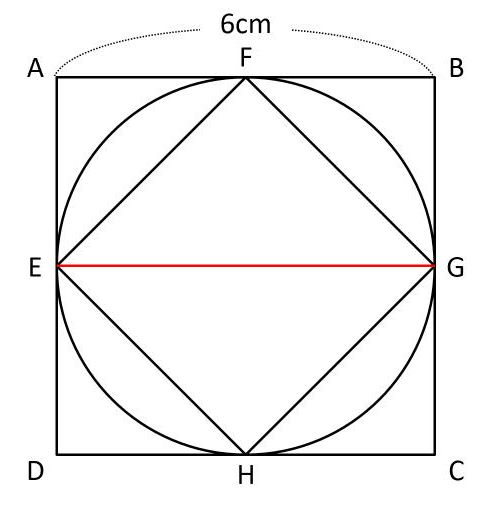



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ



数学問題 一辺100mmの正方形で 半径100mmの円の4分の1の扇形が図のよ Yahoo 知恵袋



あとまあく数学の演習 円の面積小5以上



1
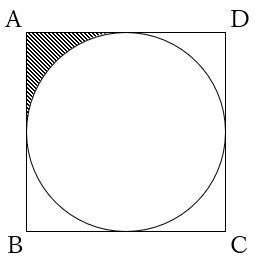



半径の分からない円の面積 中学受験プロ講師ブログ
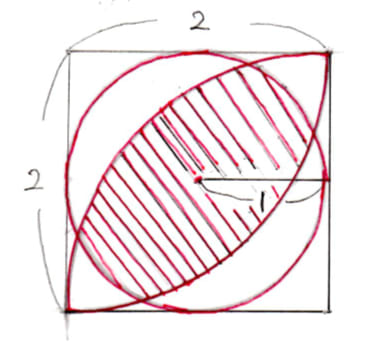



数学難問 正方形と円弧で囲まれた図形1 Takapの数学日記




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
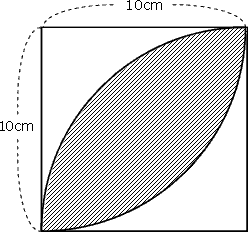



面積の求め方 算数の教え上手 学びの場 Com
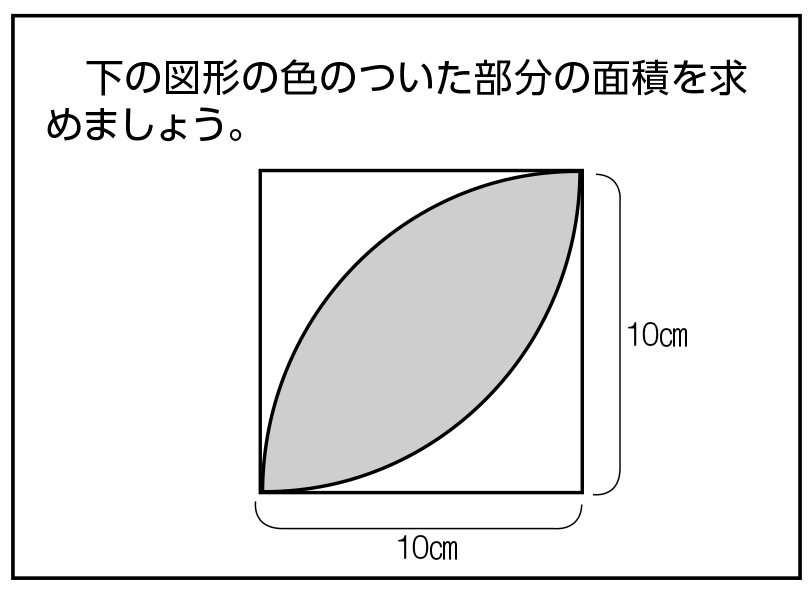



小6算数 円の面積 指導アイデア 2 みんなの教育技術
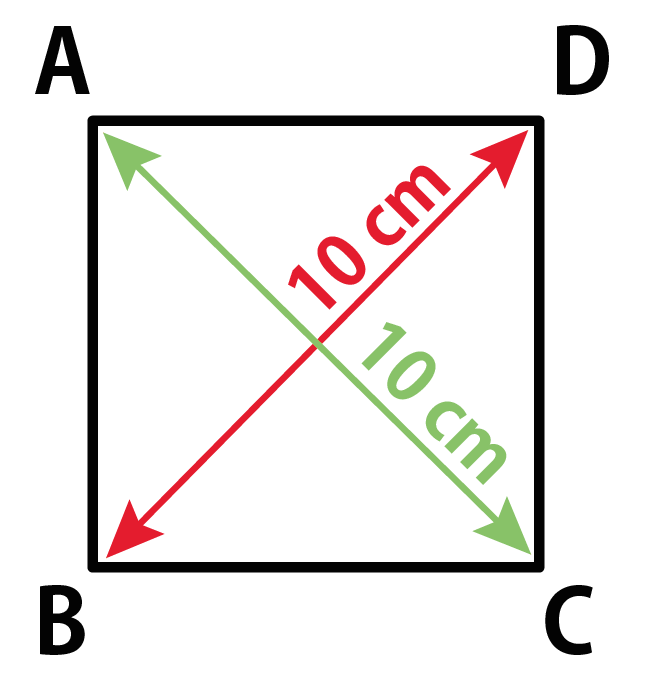



簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



4重の円の交わり 楽しいクイズの発信基地 クイズ大陸
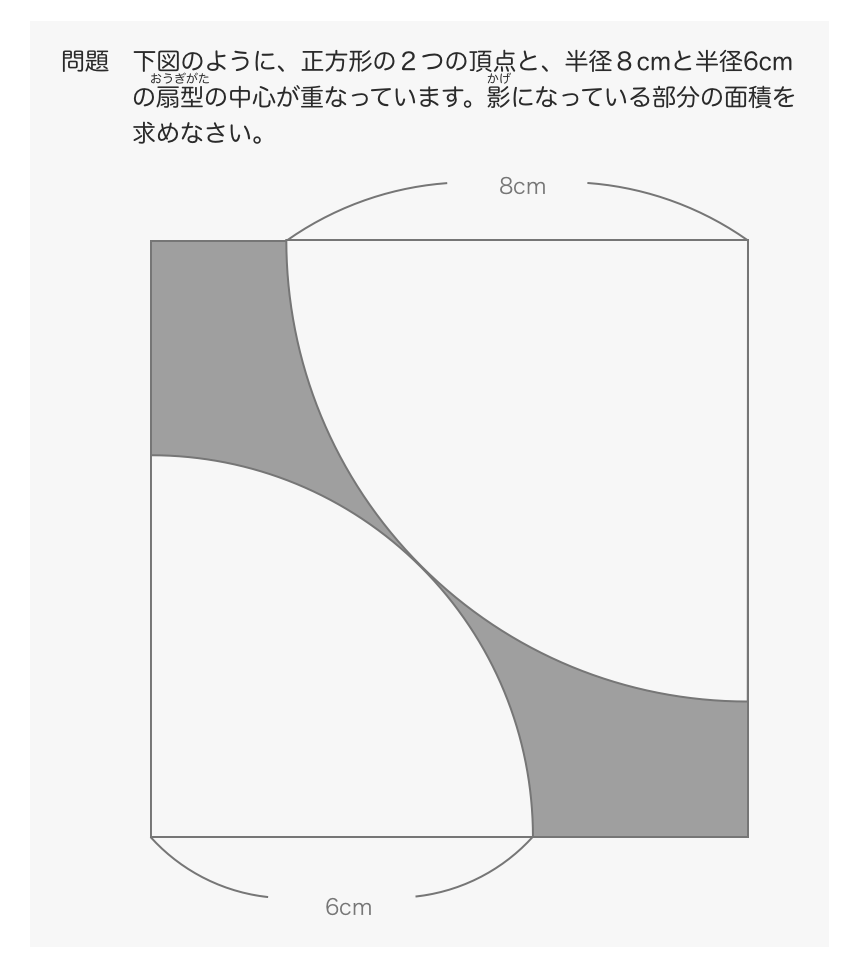



自作教材 円と扇形2 本質と技とコツ カテキョウブログ
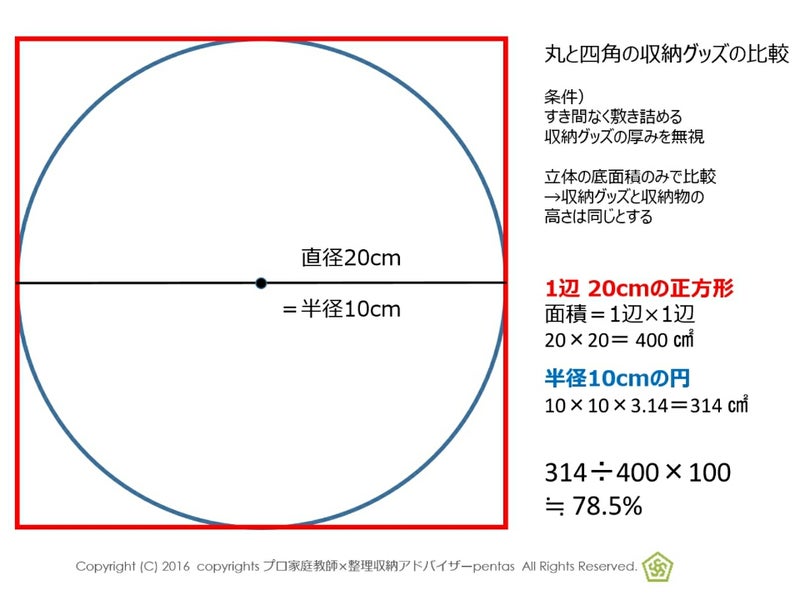



収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良



1




円の面積2 小学校6年生の教科書から 身勝手な主張
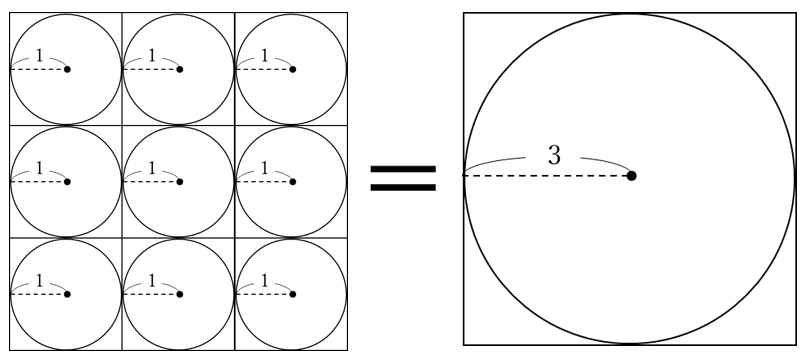



円の相似を利用した面積の計算 中学受験プロ講師ブログ




解き方わかる方がいたら教えていただきたいです ちなみに答えは32p 64です Clear



1
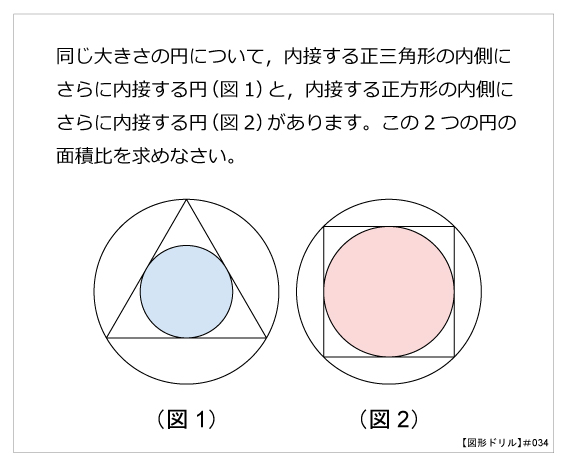



図形ドリル 第34問 内接円の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




正方形と円で囲まれた図形の面積 おわり Takapの数学日記
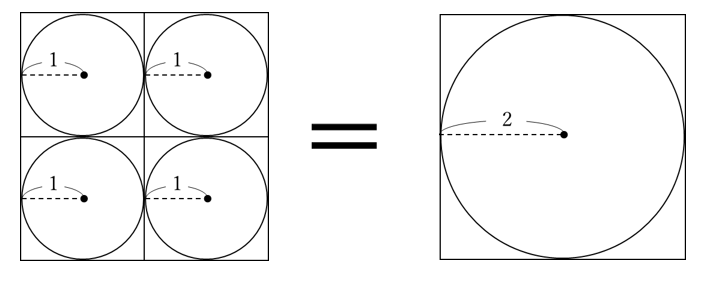



円の相似を利用した面積の計算 中学受験プロ講師ブログ




平成27年度算数教科書読み比べ 8 円の面積の求め方 わさっきhb
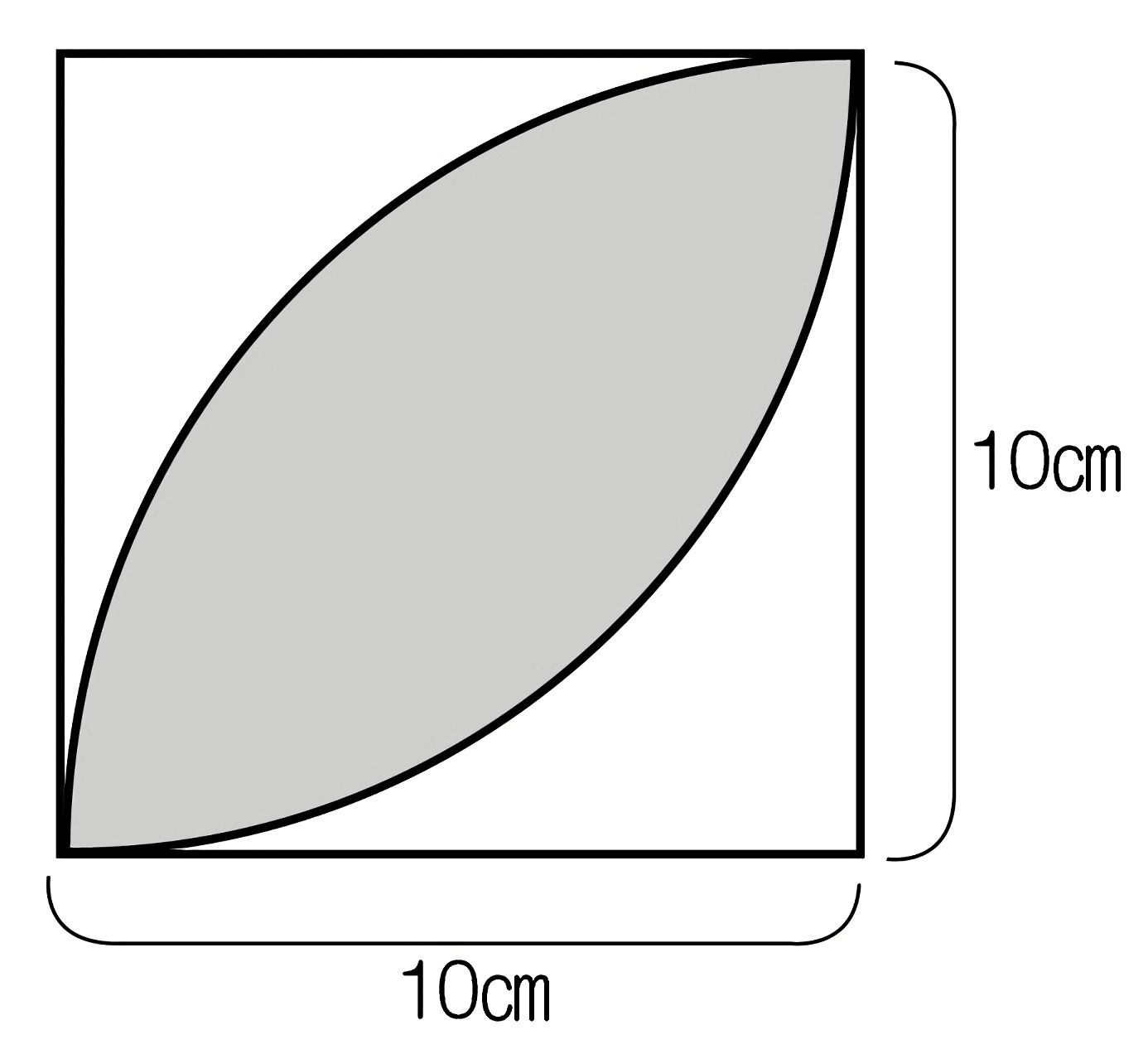



小6算数 円の面積 指導アイデア 2 みんなの教育技術



正方形の中に四分円を2つ書いたもの 影の部分のまわりの長さはcm とい Yahoo 知恵袋




直径が10 の円を切って 正方形を作りたい 正方形の長さは最大で何 になりますか Clear




標準 おうぎ形と正方形の面積 なかけんの数学ノート
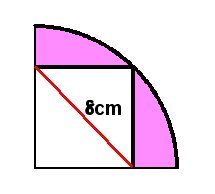



扇形と正方形



半径5cmの円の中に 下のような 正方形をかきました この正方形の 面積は何cmですか
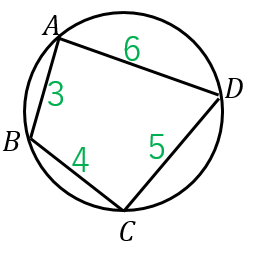



円に内接する四角形の面積を求める公式 具体例で学ぶ数学
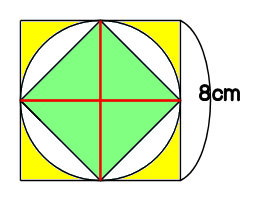



円の中の正方形 基礎



円の面積 面白ゼミナール
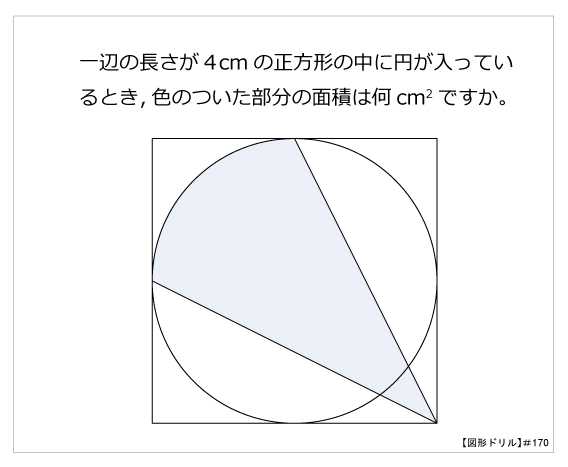



図形ドリル 第170問 円と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦




朝日新聞デジタル 円の面積 正方形を使って考えよう 山上浩二郎の大学取れたて便 大学 教育




円積問題 Wikipedia
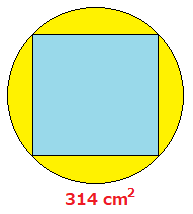



円の中の正方形の解答と解説 多目的ルーム 楽天ブログ



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




この問題教えてください 1辺がcmの正方形の内側に接している Clear



下の図は正方形の中に四分円と 半円を2つかいたものです 斜線部分の Yahoo 知恵袋



0 件のコメント:
コメントを投稿